产品详情
某同学在做加速度和力、质量的关系的实验中，测得小车的加速度a和砝码及盘的重力F的数据如下表所示：
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/（m?s-2） | 0.11 | 0.19 | 0.29 | 0.40 | 0.51 |
（2）图象的斜率的物理意义是______；
（3）图象（或延长线）与F轴的截距的物理意义是______；
（4）小车总质量为______ kg．
试题答案
解：（1）选取适当的标度，作出a-F图象如图所示．描点连线时连线性关系图象：
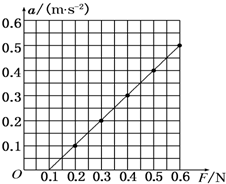
（2）由牛顿第二定律：F=Ma得：当小车质量M一定时，a与F应成正比，即：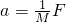
，图象应该是一条倾斜的直线，且斜率k=
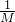，即为：小车的总质量的倒数
（3）图象与F轴的截距表示加速度恰好为零时拉力的大小，加速度恰好为零时，受力平衡，拉力就等于小车受到的阻力，即：截距是小车受到的阻力．
（4）由图可知图线斜率k=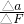
，找合适的两组数据代入（找在图象上的两个点）
，由k=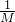可得：M=1 kg，即小车总质量为：1kg．
故答案为：（1）见上图
（2）小车的总质量的倒数
（3）小车受到的阻力
（4）1
试题解析
由牛顿第二定律：F=Ma得：当小车质量M一定时，a与F应成正比，即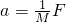：，图象应该是一条倾斜的直线，且斜率k=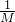，即为：小车的总质量的倒数；图象与F轴的截距表示加速度恰好为零时的拉力，也就是小车受到的阻力；根据图象我们可以求出斜率，又k=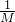，可求得M．
点评：这个实验考查的是“探究加速度和力、质量的关系”实验的实验原理：F=Ma，画出图象后对图象中的斜率截距要会根据公式进行推导明确其意义．
